ÁLGEBRA VECTORIAL

“La geometría es la ciencia del espacio puro. El álgebra es la ciencia del tiempo puro” (William Rowan Hamilton)

---

Vectores
Semántica

Un vector n-dimensional es una combinación lineal de n elementos básicos e₁, e₂, ..., e_n, es decir, la suma de los elementos básicos afectados cada uno por un coeficiente (un número real): r₁e₁ + r₂e₂ + … + r_ne_n

Esta definición es totalmente general. Pero cuando los elementos básicos son segmentos orientados en el espacio euclídeo n-dimensional, un vector se interpreta como un segmento de recta orientado y cuyas proyecciones sobre los ejes (asociados con los elementos básicos) son los coeficientes de la combinación lineal:

• Un vector en el espacio 1D (una dimensión) es un segmento lineal orientado sobre la recta real y representado por la magnitud a₁*e₁, siendo a₁ la cantidad (positiva o negativa) y e₁ el segmento unidad.
  
  
• Un vector en el espacio 2D (dos dimensiones) es un segmento lineal orientado y de proyecciones sobre los ejes a₁*e₁ y a₂*e₂, respectivamente.
  
  
• En general, un vector en el espacio nD (n dimensiones) es un segmento lineal orientado y de proyecciones sobre los ejes a₁*e₁, ... , a_n*e_n.

Sintaxis

vector en 1D: a1*e1

vector en 2D: (a1*e1 + a2*e2)

vector en 3D: (a1*e1 + a2*e2 + a3*e3)
...
vector en nD: (a1*e1 + ... + an*en)

Sintaxis alternativa como representación:

• vector en 1D: v(a1) representa a a1*e1
  
  
• vector en 2D: v(a1 a2) representa a (a1*e1 + a2*e2)
  
  
• vector en 3D: v(a1 a2 a3) representa a (a1*e1 + a2*e2 + a3*e3)
  ...
  
• vector en nD: v(a1 ... an) representa a (a1*e1 + ... + an*en)

Definición

⟨( v(a1…an) =: +⊣( ⌊a1…an⌋*⌊e1…en⌋ ) )⟩

Ejemplos

1. v(13 10) // rep. (13*e1 + 10*e2)
   
   
2. v(a b c) // rep. (a*e1 + b*e2 + c*e3)
   
   
3. v(-1 x 2 y) // rep. (-e1 + x*e2 + 2*e3 + y*e4)
   
   
4. v(0) // ev. 0 (el vector cero se evalúa como cero)

Observaciones

• La definición formal de vector no especifica que se trate de un elemento geométrico. La interpretación geométrica es la habitual, pero en MENTAL la expresiones ai y ei podrían ser cualesquiera.
  
  
• La sintaxis alternativa evita el tener que especificar cada vez la combinación lineal, pues nos basta con especificar los coeficientes de dicha combinación lineal. Esta notación puede, evidentemente, ser sustituida por cualquier otra. Por ejemplo, utilizando v como calificador, como en (a1 a2)/v. La notación elegida corresponde a vector como función de sus componentes.
  
  
• En la definición de la sintaxis alternativa se utiliza la sustitución potencial, lo que indica que se trata de una representación.
  
  
• A veces es más cómodo la representación directa, que evita especificar ceros, como por ejemplo, 27*e4, en lugar de v(0 0 0 27).
  
  
• Los vectores básicos e1, ... , en, así como v, se podrían especificar en cursiva para diferenciarlos de las variables ordinarias.
  
  
• Los elementos e1, ..., en se denominan también vectores básicos o generadores, pues por combinación lineal de ellos se obtienen todos los vectores posibles. Se tiene:
  
  
  (v(1) =: e1)
(v(0 1) =: e2)
(v(0 0 1) =: e3)
  etc.
  
  
• De acuerdo con la definición, si los vectores tienen diferentes longitudes, se suponen ceros a la derecha del vector más corto. Por ejemplo,
  
  
  (v(1 2 3) + v(4 5)) // eq. (v(1 2 3) + v(4 5 0)) ev. v(5 7 3)
  
  
• Los vectores se pueden utilizar en el lenguaje como cualquier otra expresión. Pueden aparecer en expresiones genéricas, en secuencias, en conjuntos, etc. Por ejemplo:
  
  
  Secuencia.
  ( (13 25) v(1 2 3) {a b} )
  
  Expresión genérica parametrizada.
  ⟨( f(x) = v(x 2*x 3*x) )⟩
  
  
• El conjunto de todos los vectores posibles de n dimensiones forman un espacio vectorial n-dimensional.

Operaciones con vectores

Hay dos operaciones fundamentales con los vectores:

1. Suma.
   La suma de dos vectores es otro vector cuyos componentes son la suma de los componentes correspondientes de cada uno de los vectores.
   
   
2. Producto por un factor.
   El producto de un factor por un vector es otro vector de componentes iguales al del vector multiplicadas por dicho factor.

Estas operaciones no hace falta definirlas, pues resultan de las propiedades de la suma y del producto.

Ejemplos:

1. (e1 + 2*e2 + 3*e3)+(4*e1 + 5*e2 + 6*e3) // rep. (5*e1 + 7*e2 + 9*e3) rep. v(5 7 9)
   
   
2. (v(1 2 3) + v(4 5 6)) // ev. v(5 7 9)
   
   
3. 2*(e1 + 2*e2 + 3*e3) // ev. v(2 4 6) rep. (2*e1 + 4*e2 + 6*e3)
   
   
4. 2*(v(1 2 3)) // ev. v(2 4 6)
   
   
5. (v(3 4 7) + 2*e1) // ev. v (5 4 7)

Propiedades

(Suponemos que los nombres de los vectores empiezan por “v”).

1. Conmutativa.
   ⟨( v1+v2 ≡ v2+v1 )⟩
   
   
2. Conmutativa respecto a un factor.
   ⟨( r*v = v*r )⟩
   
   
3. Asociativas,
   ⟨( (v1+v2)+v3 ≡ v1+(v2+v3) )⟩
   
   
4. Distributivas.
   ⟨( r*(v1 + v2) ≡ (r*v1 + r*v2) )⟩

⟨( (v1 + v2)*r ≡ (v1*r + v2*r) )⟩

⟨( (r1 + r2)*v ≡ (r1*v + r2*v) )⟩

⟨( v*(r1 + r2) ≡ (v*r1 + v*r2) )⟩
   
   
5. Vector contrario.
   ⟨( −v ≡ (−1)*v )⟩
   
   
6. Vector cero.
   ⟨( v(0) = 0 )⟩
   
   
7. ⟨( v−v = 0 )⟩

Vectores de orden superior

Un vector puede, evidentemente, contener otros vectores. Los vectores descritos hasta ahora son de orden 1. A los escalares (números) se suelen denominarles vectores de orden cero. Un vector que contiene un vector de orden 1 es de orden 2. En general, un vector que contiene un vector de orden n es de orden n+1. Ejemplos:

1. v(v(1 2 3) v(4 5 6)) // ev. ((v(1 2 3))*e1 + (v(4 5 6))*e2) ev. ((e1 + 2*e2 + 3*e3)*e1 + (4*e1 + 5*e2 + 6*e3)*e2) ev. (e1*e1 + 2*e2*e1 + 3*e3*e1 + 4*e1*e2 + 5*e2*e2 + 6*e3*e2) (e1^2 + 6*e2*e1 + 3*e3*e1 + 5*e2^2 + 6*e3*e2)
   
   
2. v(v(v(1 2 3))) // ev. (v(v(1 2 3)))*e1 ev. v(1 2 3)*e1*e1 ev. (e1 + 2*e2 + 3*e3)*e1*e1 ev. (e1*e1*e1 + 2*e2*e1*e1 + 3*e3*e1*e1 ev. (e1^3 + 2*e2*e1^2 + 3*e3*e1^2)

Propiedades:

1. Multiplicación por un factor.
   (v(v1 v2))*r =: v(v1*r v2*r) )
   
   
2. Suma de vectores.
   ( (v(v1 v2) + v(v3 v4)) =: v(v1+v3 v2+v4))

Producto Interno de Dos Vectores
Semántica

El producto interno de dos vectores v1 y v2 es el producto algebraico o aritmético de ambos vectores, pero con la interpretación del producto de los vectores básicos ei*ej como la proyección del vector ei sobre el ej (o viceversa). En el espacio euclídeo, como los vectores básicos son perpendiculares entre sí, entonces (ei*ej = 1) si i=j y (ei*ej = 0) si i≠j.

En el caso de vectores de orden 1, el producto interno se denomina “producto escalar” y es la suma de los productos de los componentes correspondientes de ambos vectores.


Sintaxis

Como se trata de un atributo de la operación producto, lo podemos simbolizar mediante la expresión (v1 */i v2), que indica producto vectorial interno de los vectores v1 y v2.


Definición

⟨( v1 */vi v2 = (v1*v2)/Proy )⟩

siendo Proy la interpretación “proyección”, es decir:

( Proy = ⟨( (ei*ej = (1 ← i=j →' 0) )⟩ )

La función delta de Kronecker se define así:

⟨( δ(i j) = (1 ← i=j →' 0) )⟩

Por lo tanto,

⟨( (v1 */vi v2) = v1*v2/(ei*ej = δ(i j) )⟩

Ejemplos

1. El resultado es un escalar.
   (v(1 2 3) */vi v(4 5 6)) // ev. (1*4 + 2*5 + 3*6) ev. 32
   
   
2. El resultado es un vector.
   (v(1 2) v(3 4)) */vi v(5 6) // ev. ((v(1 2))*5 + (v(3 4))*6) ev. (v(5 10) + v(18 24)) ev. v(23 34)

Observaciones

• El producto interno de dos vectores perpendiculares en el espacio euclídeo es el escalar cero. Por ejemplo, en 2D, el producto interno del vector v(a b) por el rotado 90º (en el sentido contrario al de las agujas del reloj), que es v(−b a), es cero:
  
  
  (v(a b) */vi v(−b a)) // ev. 0
  
  
• El producto interno de un vector de orden n por otro vector de nivel 1 es un vector de orden n−1.
  
  
• Las expresiones utilizadas ei*ej = 0 o 1, y la función delta de Kronecker son imaginarias, de acuerdo con la definición de expresión imaginaria en MENTAL.

Propiedades

1. Conmutativa.
   ⟨( (v1 */vi v2) ≡ (v2 */vi v1) )⟩
   
   
2. Transposición de un factor.
   ⟨( f*(v1 */vi v2) ≡ (v1 */vi f*v2) )⟩
⟨( f*(v1 */vi v2) ≡ (f*v1 */vi v2) )⟩
   
   
3. Distribución respecto a la suma.
   ⟨( (v1 */vi (v2+v3)) ≡ ((v1 */vi v2) + (v1 */vi v3)) )⟩
   
   
4. El producto interno de un vector por cero es cero.
   ⟨( (v */vi 0) = 0 )⟩

Módulo de un vector

Por definición, el módulo de un vector v de orden 1, que podemos representar por mod(v), es:

⟨( mod(v) = (v */vi v)V2 )⟩
(recuérdese que x^vn es ⁿ√x)

Ejemplo: mod(v(3 4)) // ev. 5

El módulo de un vector de orden 1 corresponde a su longitud en el espacio nD, de acuerdo con el teorema de Pitágoras: la raíz cuadrada de la suma de los cuadrados de los componentes Y se cumple también la propiedad de Cauchy-Schwarz:

⟨( v1 */vi v2 ≤ mod(v1)*mod(v2) )⟩

Producto Externo de Dos Vectores
Semántica

El producto externo de dos vectores v1 y v2, en el espacio nD, es el producto algebraico o aritmético de ambos vectores, pero con interpretación del producto de los vectores básicos ei*ej como la superficie del paralelogramo formado por los vectores ei y ej. La superficie está orientada, es decir, tiene signo, con el criterio siguiente: si i<j, entonces la superficie es ei*ej. Si i>j, entonces ei*ej es −(ej*ei). Evidentemente, (ei*ei = 0).



Sintaxis

Como se trata de un atributo de la operación producto, lo vamos a simbolizar mediante la expresión (v1 */ve v2), que indica el producto vectorial externo de los vectores v1 y v2.


Definición

⟨( v1 */ve v2 = (v1*v2)/Sup )⟩

Siendo Sup la interpretación “superficie”, es decir:

(Sup = ⟨( (ei*ej = (0 ← i=j →' (ei*ej ← i<j →' −(ej*ei)) )⟩)

Ejemplos

1. En el espacio 2D tenemos:
   
   

   */ve	e1	e2
   e1	0	e1*e2
   e2	−e1*e2	0

   
   ( v1 = v(a1 a2) ) // rep. (a1*e1 + a2*e2)

( v2 = v(b1 b2) ) // rep. (b1*e1 + b2*e2)

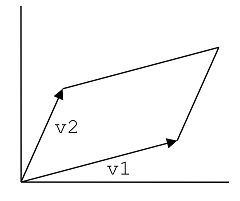
(v1 */ve v2) // ev. (a1*b2 − a2*b1)*(e1*e2)
   
   El resultado es una magnitud de cantidad (a1*b2 − a2*b1) y unidad (e1*e2). La cantidad representa la superficie del paralelogramo formado por los dos vectores (ver figura). La cantidad es también el valor del determinante:
   
   

   |a1	a2|
   |b1	b2|

   
   
2. En el espacio 3D tenemos:
   
   

   */ve	e1	e2	e3
   e1	0	e1*e2	e1*e3
   e2	−e1*e2	0	e2*e3
   e3	−e1*e3	−e2*e3	0

   
   ( v1 = v(a1 a2 a3) ) // rep. (a1*e1 + a2*e2 + a3*e3)

( v2 = v(b1 b2 b3) ) // rep. (b1*e1 + b2*e2 + b3*e3)

(v1 */ve v2) // ev. ( (a1*b2 − a2*b1)*(e1*e2) +
(a2*b3 − a3*b2)*(e2*e3) +
(a1*b3 − a3*b1)*(e1*e3) )
   
   Llamando
   
   ⟨( S(i j) =: (ai*bj − aj*bi) )⟩
   
   a la superficie formada por los vectores i y j proyectada sobre el plano formado por los vectores unitarios ei y ej, se tiene:
   
   
   ( (v1 */ve v2) ≡ (S(1 2)*e1*e2 + S(2 3)*e2*e3 + S(1 3)*e1*e3 )
   
   
3. En el espacio 4D tenemos:
   
   

   */ve	e1	e2	e3	e4
   e1	0	e1*e2	e1*e3	e1*e4
   e2	−e1*e2	0	e2*e3	e2*e3
   e3	−e1*e3	−e2*e3	0	e3*e4
   e4	−e1*e4	−e2*e4	−e3*e4	0

   
   ( v1 = v(a1 a2 a3 a4) ) // rep. (a1*e1 + a2*e2 + a3*e3 + a4*e4)

( v2 = v(b1 b2 b3 b4) // rep. (b1*e1 + b2*e2 + b3*e3 + b4*e4)

( (v1 */ve v2) ≡ (Sup(1 2)*e1*e2 + Sup(1 3)*e1*e3 +
Sup(1 4)*e1*e4 + Sup(2 3)*e2*e3 +
Sup(2 4)*e2*e4 + Sup(3 4)*e3*e4 )

En general, el producto externo de dos vectores en el espacio nD es la suma de las proyecciones del paralelogramo formado por los dos vectores sobre los planos correspondientes a las combinaciones de los n elementos básicos tomados de 2 en 2.


Propiedades

1. El autoproducto externo es cero.
   ⟨( (v */ve v) = 0 )⟩
   
   
2. Anticonmutatividad.
   < ⟨( (v1 */ve v2) ≡ −(v2 */ve v1) )⟩
   
   
3. Distribución respecto a la suma.
   ⟨( (v1 */ve (v2+v3)) ≡ (v1 */ve v2) + (v1 */ve v3) )⟩
   
   
4. Dependencia lineal.
   ⟨( (v1 = r*v2) → (v1 */ve v2 = 0) )⟩

Observaciones

• La interpretación tradicional en el espacio 3D del producto de dos vectores es otro vector perpendicular a ambos y de sentido regido por la ley del sacacorchos. Y el producto de los vectores unitarios es: e₁e₂ = e₃, e₂e₃ = e₁ e₃e₁ = e₂
  
  Estas leyes son las mismas que rigen a los cuaterniones de Hamilton: ij = k, jk = i, ki = j. De hecho, el concepto de vector proviene históricamente de los cuaterniones.

Multivectores
Semántica

El concepto de multivector generaliza dos cosas: por una parte, el concepto de vector, y por otra el producto externo de dos vectores, ampliándolo a cualquier número m de vectores, siendo 1≤m≤n y n la dimensión del espacio.

• Un 0-vector es un escalar (número).
  
• Un 1-vector es un vector tradicional (segmento lineal orientado).
  
• Un 2-vector (o bivector) es un segmento de plano orientado.
  
• Un 3-vector (o trivector) es un segmento de volumen orientado.
  
• Un m-vector es un segmento de hipervolumen de dimensión m orientado.

Multivectores básicos

Un multivector de orden m se expresa como combinación lineal de los multivectores básicos de orden m. Por ejemplo, en el espacio 3D, tenemos los siguientes multivectores básicos:

• De orden 1, corresponden a los tres subespacios unidimensionales (1, 2 y 3): e1 e2 e3
  
  
• De orden 2, corresponden a los tres subespacios bidimensionales (1-2, 1-3 y 2-3): e1*e2 e1*e3 e2*e3
  
  
• De orden 3, corresponden al espacio de dimensión 3: e1*e2*e3. Se verifica que:
  
  
  e2*e3*e1 = e3*e1*e2 = e1*e2*e3

e1*e3*e2 = e3*e2*e1 = e2*e1*e3 = −e1*e2*e3
  
  Es decir, las permutaciones circulares son iguales.

Los multivectores básicos también se suelen representar con la letra e seguida de los números de los componentes. Por ejemplo:

(e12 =: e1*e2)
(e123 =: e1*e2*e3)

Así que en el espacio 3D tenemos los multivectores básicos:

e1 e2 e3 e12 e13 e23 e123

Ejemplos

En el espacio 3D:

• 0-vector: 17
  
  
• 1-vector: (3*e1 + 4*e2 + 5*e3)
  
  
• 2-vector: (3*e12 + 4*e13 + 5*e23)
  
  
• 3-vector: 3*e123

En el espacio 4D:

• 0-vector: 17
  
  
• 1-vector: (3*e1 + 4*e2 + 5*e3 + 6*e4)
  
  
• 2-vector: (3*e12 + 4*e13 + 5*e14 + 6*e23 + 7*e24 + 8*e34)
  
  
• 3-vector: (3*e123 + 3*e124 + 3*e234)
  
  
• 4-vector: 7*e1234

Producto externo de multivectores

Hemos visto que el producto externo de dos vectores en el espacio 2D es la superficie formada por dichos vectores es una magnitud cuya cantidad es el valor de un determinante de orden 2, y cuya unidad es e1*e2. Corresponde a un 2-vector (bivector). Análogamente, el producto externo de tres vectores (trivector) (a, b y c) en el espacio 3D captura el volumen del espacio del paralelepípedo formado por dichos vectores, cuya cantidad es igual el valor del determinante de orden 3:

|a1	a2	a3|
|b1	b2	b3|
|c1	c2	c3|

y cuya unidad es e1*e2*e3.

En general, el hipervolumen encerrado por m vectores v1, ... ,vm en el espacio nD es el determinante de orden m. Es la llamada “fórmula de Gauss”. Corresponde al multivector (m-vector) (v1 */ve ... */ve vm) en el espacio nD (siendo m≤n). Abreviadamente: (*/ve)⊣(v1…vm).


Números vs.Vectores
Números compuestos como vectores

Un número compuesto, por ejemplo, n=(7 12 54 3), cuyo valor normalizado n. (n con punto decimal) es

(7*(10^3) + 12*(10^2) + 54*10 + 3) ev. 8743

se comporta, a todos los efectos, como un vector. En efecto:

1. Es una combinación lineal de expresiones básicas. Las expresiones básicas son: e1=1, e2=10, (e3 = 10^2), etc. En general, ⟨( ei = 10^(i−1) )⟩
   
   
2. Cumple todas las propiedades de un espacio vectorial. En particular, cumple la propiedad distributiva respecto a la multiplicación por un factor:
   
   2*(7 12 54 3). eq. (2*7 2*12 2*54 2*3). eq. (14 24 108 6). eq. 17486 eq. 2*8743
   
   Y la propiedad distributiva lineal respecto a la suma:
   
   ((7 12 54 3). + (6 89 4).) ev. 8743+1494 ev. 10237
(7+0 12+6 54+89 3+4). ev. (7 18 143 7). ev. 10237

Observaciones:

1. En los vectores, los vectores básicos se numeran de izquierda a derecha. En los números es al revés: se numeran de derecha a izquierda. Por ello, los componentes básicos de un número que no existen a la izquierda, son cero.
   
   
2. Los números con el punto decimal a la izquierda también son vectores.
   
   
3. Los números de orden superior (los compuestos de dos o más niveles) funcionan de forma análoga.

Vectores en Funciones
Con los vectores se pueden definir funciones en las que los argumentos y/o el resultado pueden ser vectores.

Ejemplos:

1. ⟨( f(v) = (v(1 2 3) */vi v) )⟩
f(v(11 12 13)) // ev. (1*11 + 2*12 + 3*13) ev. 74
   
   
2. ⟨( v(t) = v(t t+1 t+2))⟩ // velocidad (vector) en función del tiempo (escalar)
v(10) // ev. v(10 11 12)
   
   
3. ⟨( f(v(r1 r2 r3)) = v(r1+r2 r1+r3 r2+r3) )⟩
   
   El argumento v(r1 r2 r3) es un vector que representa un punto del espacio 3D. El resultado es otro vector. En este caso tenemos lo que se denomina un “campo vectorial”.
   
   f(v(2 3 4)) // ev. v(2+3 2+4 3+4) ev. v(5 6 7)
   
   
4. ⟨( f(v(x y z)) = (x*a + y*b + z*c) )⟩
   Función que asigna a cada vector un escalar.
   
   f(v(2 3 4)) // ev. 2*a + 3*b + 4*c

---

Adenda
Magnitudes físicas

Las magnitudes físicas pueden ser escalares o vectoriales.

• Una magnitud escalar es la que puede representarse mediante un único valor numérico (junto con su correspondiente unidad), por ejemplo, la masa, la temperatura, etc., y es independiente del sistema de coordenadas utilizado.
  
  
• Una magnitud vectorial necesita, además de un valor numérico (y también su correspondiente unidad) su dirección en el espacio, por ejemplo, la velocidad, la fuerza, el campo eléctrico, el campo magnético, etc. La forma más sencilla y uniforme de representar un vector es mediante una secuencia de números, que corresponden a los componentes del vector respecto a cada dimensión del espacio. Un vector se puede considerar como un “número dirigido”, como un “supernúmero” o como un “número multidimensional”.

Bibliografía

• Anton, Howard. Elementary Linear Algebra (Applications Version). Wiley International, 2005.
  
  
• Brand, Louis. Análisis vectorial. Compa⟩ía Editorial Continental, S.A. (CECSA),México, 1959.
  
  
• Castellet, Manuel; Llerena, Irene. álgebra lineal y geometría. Editorial Reverté, 2000.
  
  
• Crowe, M.J. A History of Vector Analysis. Dover, 1994.
  
  
• Halmos, P.R. Finite-Dimensional Vector Spaces. D. van Nostrand, 1958. (Pese a su antigüedad, es uno de los mejores libros sobre espacios vectoriales finito-dimensionales. Está escrito en un estilo simple y coloquial.)
  
  
• Bretscher, Otto. Linear Algebra with Applications. Prentice Hall, 2004.
  
  
• Kemmer, N. Análisis vectorial. Editorial Reverté, 2004.
  
  
• Marsden, Jerrold; Tromba, Anthony. Cálculo vectorial. Pearson Addison-Wesley, 2007.
  
  
• Ricardo, Henry. A Modern Introduction To Linear Algebra. CRC Press, 2010.
  
  
• Scala Estalella, Juan José. Análisis Vectorial. Vectores. Editorial Síntesis, 1995.